Advertisements
Advertisements
Question
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Solution
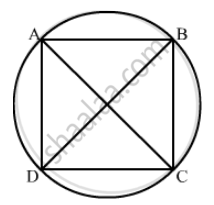
To prove: AC = BD
Proof: We know that equal chords subtend equal at the centre of circle and the angle subtended by a chord at the centre is twice the angle subtended by it at remaining part of the circle.
\[\angle AOD = \angle BOC \left( \text{ O is the centre of the circle } \right)\]
\[\angle AOD = 2\angle ACD \]
\[\text{ and } \angle BOC = 2\angle BDC\]
\[\text{ Since, } \angle AOD = \angle BOC\]
\[ \Rightarrow \angle ACD = \angle BDC . . . . . \left( 1 \right) \]
\[\angle ACB = \angle ADB . . . . . \left( 2 \right) \left( \text{ Angle in the same segment are equal } \right)\]
\[\text{ Adding } \left( 1 \right) \text{ and } \left( 2 \right)\]
\[\angle BCD = \angle ADC . . . . . \left( 3 \right)\]
\[\text{ In } \bigtriangleup ACD \text{ and } \bigtriangleup BDC\]
\[CD = CD \left( \text{ common } \right)\]
\[\angle BCD = \angle ADC \left[ \text{ Using } \left( 3 \right) \right]\]
\[AD = BC \left( given \right)\]
\[\text{ Hence } , \bigtriangleup ACD \cong BDC \left( \text{ SAS congruency criterion } \right)\]
\[ \therefore AC = BD \left( \text{ cpct } \right)\]
Hence Proved
APPEARS IN
RELATED QUESTIONS
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

Find all the angles of the given cyclic quadrilateral ABCD in the figure.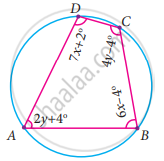
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
