Advertisements
Advertisements
Question
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

Solution
£ADE = 95°(Given) Since,
OA = OB, so
∠OAB = ∠OBA
∠OAB = 30°
∠ADE + ∠ADC = 180°
(Linear pair)
95° + ∠ADC = 180°
∠ADC = 85°
We know that,
∠ADC = 2∠ADC
∠ADC = 2 x 85°
∠ADC = 170°
Since,
AO = OC
(Radii of circle)
∠OAC = ∠OCA
(Sides opposite to equal angle) ... (i)
In triangle OAC,
∠OAC + ∠OCA + ∠AOC = 180°
∠OAC + ∠OAC + 170° = 180°
[From (i)]
2∠OAC = 10°
∠OAC = 5°
Thus,
∠OAC = 5°
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
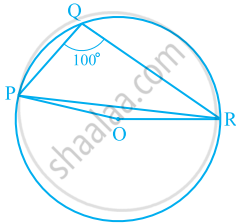
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
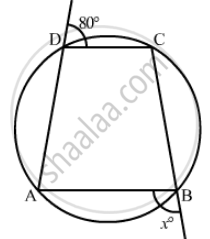
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
