Advertisements
Advertisements
Question
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution
Draw OM ⊥ AB and ON ⊥ CD. Join OB and OD.
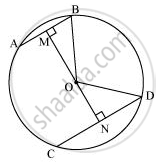
BM = AB/2 = 5/2 (Perpendicular from the centre bisects the chord)
ND = CD/2 = 11/2
Let ON be x. Therefore, OM will be 6− x.
In ΔMOB,
OM2 + MB2 = OB2
(6 - x)2 + (5/2)2 = OB2
36 + x2 - 12x + 25/4 = OB2 ........(1)
In ΔNOD,
ON2 + ND2 = OD2
x2 + (11/2)2 = OD2
x2 + 121/4 = OD2 .........(2)
We have OB = OD (Radii of the same circle)
Therefore, from equation (1) and (2),
`36+x^2-12x+25/4=x^2+121/4`
`12x=36+24/4-121/4`
`=(144+25-121)/4`
`=48/4`
= 12
x = 1
From equation (2),
`(1)^2+(121/4)=OD^2`
`OD^2 = 1+121/4=125/4`
`OD=5/2sqrt5`
Therefore, the radius of the circle is `5/2sqrt5" cm."`
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
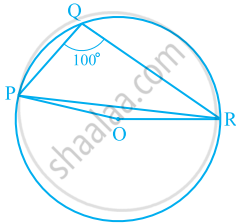
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

Find all the angles of the given cyclic quadrilateral ABCD in the figure.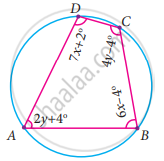
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
