Advertisements
Advertisements
प्रश्न
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
उत्तर
Draw OM ⊥ AB and ON ⊥ CD. Join OB and OD.
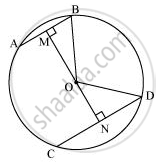
BM = AB/2 = 5/2 (Perpendicular from the centre bisects the chord)
ND = CD/2 = 11/2
Let ON be x. Therefore, OM will be 6− x.
In ΔMOB,
OM2 + MB2 = OB2
(6 - x)2 + (5/2)2 = OB2
36 + x2 - 12x + 25/4 = OB2 ........(1)
In ΔNOD,
ON2 + ND2 = OD2
x2 + (11/2)2 = OD2
x2 + 121/4 = OD2 .........(2)
We have OB = OD (Radii of the same circle)
Therefore, from equation (1) and (2),
`36+x^2-12x+25/4=x^2+121/4`
`12x=36+24/4-121/4`
`=(144+25-121)/4`
`=48/4`
= 12
x = 1
From equation (2),
`(1)^2+(121/4)=OD^2`
`OD^2 = 1+121/4=125/4`
`OD=5/2sqrt5`
Therefore, the radius of the circle is `5/2sqrt5" cm."`
APPEARS IN
संबंधित प्रश्न
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
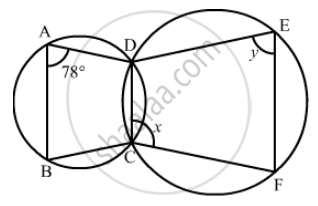
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
