Advertisements
Advertisements
प्रश्न
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
Advertisements
उत्तर
Given:
ABCD is a trapezium whose non-parallel sides AD and BC are equal.
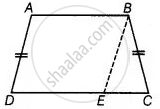
Trapezium ABCD is cyclic.
Join BE, where BE || AD
Proof: Since, AB || DE and AD || BE
Since the quadrilateral ABED is a parallelogram.
∴ ∠BAD = ∠BED ...(i) [Opposite angles of a parallelogram are equal]
And AD = BE ...(ii) [Opposite angles of a parallelogram are equal]
But AD = BC [Given] ...(iii)
From equations (ii) and (iii)
BC = BE
⇒ ∠BEC = ∠BCE ...(iv) [Angles opposite to equal sides are equal]
Also, ∠BEC + ∠BED = 180° ...[Linear pair axiom]
∴ ∠BCE + ∠BAD = 180° ...[From equations (i) and (iv)]
If the sum of opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic.
Hence, trapezium ABCD is cyclic.
Hence proved.
संबंधित प्रश्न
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
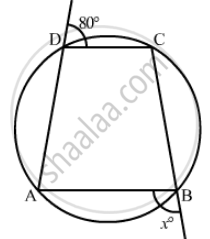
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.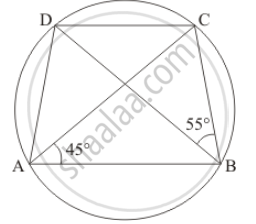
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
