Question

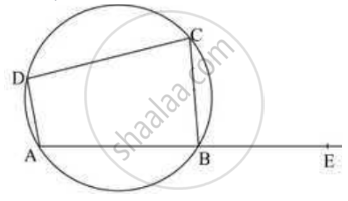
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.

Answer 1

In ΔAOD and ΔCOE,

OA = OC (Radii of the same circle)

OD = OE (Radii of the same circle)

AD = CE (Given)

∴ ΔAOD ≅ ΔCOE (SSS congruence rule)

∠OAD = ∠OCE (By CPCT) ... (1)

∠ODA = ∠OEC (By CPCT) ... (2)

Also,

∠OAD = ∠ODA (As OA = OD) ... (3)

From equations (1), (2), and (3), we obtain

∠OAD = ∠OCE = ∠ODA = ∠OEC

Let ∠OAD = ∠OCE = ∠ODA = ∠OEC = x

In Δ OAC,

OA = OC

∴ ∠OCA = ∠OAC (Let a)

In Δ ODE,

OD = OE

∠OED = ∠ODE (Let y)

ADEC is a cyclic quadrilateral.

∴ ∠CAD + ∠DEC = 180° (Opposite angles are supplementary)

x + a + x + y = 180°

2x + a + y = 180°

y = 180º − 2x − a ... (4)

However, ∠DOE = 180º − 2y

And, ∠AOC = 180º − 2a

∠DOE − ∠AOC = 2a − 2y = 2a − 2 (180º − 2x − a)

= 4a + 4x − 360° ... (5)

∠BAC + ∠CAD = 180º (Linear pair)

⇒ ∠BAC = 180º − ∠CAD = 180º − (a + x)

Similarly, ∠ACB = 180º − (a + x)

In ΔABC,

∠ABC + ∠BAC + ∠ACB = 180º (Angle sum property of a triangle)

∠ABC = 180º − ∠BAC − ∠ACB

= 180º − (180º − a − x) − (180º − a −x)

= 2a + 2x − 180º

= 1/2[4a + 4x − 360°]

∠ABC = 1/2[∠DOE − ∠ AOC] [Using equation (5)]