Advertisements
Advertisements
प्रश्न
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
उत्तर
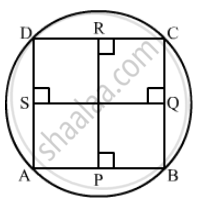
To prove: Perpendicular bisector of side AB, BC, CD and DA are concurrent i.e, passes through the same point.
Proof:
We know that the perpendicular bisector of every chord of a circle always passes through the centre.
Therefore, Perpendicular bisectors of chord AB, BC, CD and DA pass through the centre which means they all passes through the same point.
Hence, the perpendicular bisector of AB, BC, CD and DA are concurrent.
APPEARS IN
संबंधित प्रश्न
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

If non-parallel sides of a trapezium are equal, prove that it is cyclic.
