Advertisements
Advertisements
प्रश्न
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
उत्तर
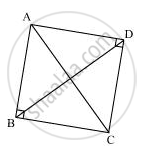
In ΔABC,
∠ABC + ∠BCA + ∠CAB = 180° ...(Angle sum property of a triangle)
⇒ 90° + ∠BCA + ∠CAB = 180°
⇒ ∠BCA + ∠CAB = 90° ...(1)
In ΔADC,
∠CDA + ∠ACD + ∠DAC = 180° ...(Angle sum property of a triangle)
⇒ 90° + ∠ACD + ∠DAC = 180°
⇒ ∠ACD + ∠DAC = 90° ...(2)
Adding equations (1) and (2), we obtain
∠BCA + ∠CAB + ∠ACD + ∠DAC = 180°
⇒ (∠BCA + ∠ACD) + (∠CAB + ∠DAC) = 180°
∠BCD + ∠DAB = 180° ...(3)
However, it is given that
∠B + ∠D = 90° + 90° = 180° ...(4)
From equations (3) and (4), it can be observed that the sum of the measures of opposite angles of quadrilateral ABCD is 180°. Therefore, it is a cyclic quadrilateral.
Consider chord CD.
∠CAD = ∠CBD ...(Angles in the same segment)
APPEARS IN
संबंधित प्रश्न
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
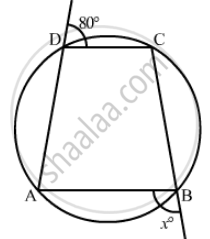
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
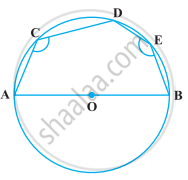
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
