Advertisements
Advertisements
प्रश्न
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
उत्तर
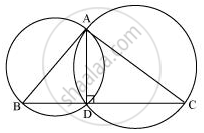
Consider a ΔABC.
Two circles are drawn while taking AB and AC as the diameter.
Let they intersect each other at D and let D not lie on BC.
Join AD.
∠ADB = 90° ...(Angle subtended by semi-circle)
∠ADC = 90° ...(Angle subtended by semi-circle)
∠BDC = ∠ADB + ∠ADC = 90° + 90° = 180°
Therefore, BDC is a straight line and hence, our assumption was wrong.
Thus, Point D lies on third side BC of ΔABC.
APPEARS IN
संबंधित प्रश्न
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
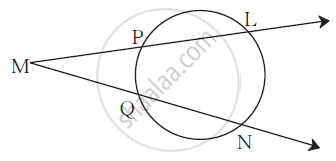
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
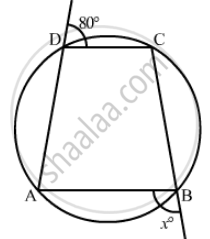
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.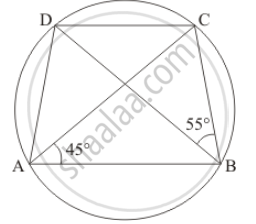
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
