Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.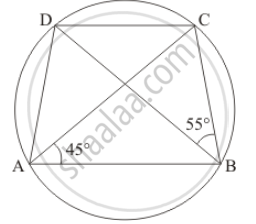
उत्तर
It is given that ABCD is a cyclic quadrilateral with AC and DB as its diagonals.
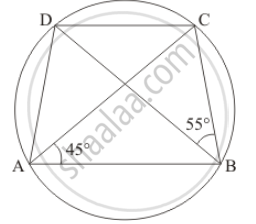
We have to find `angleBCD`
Since angles in the same segment of a circle are equal
So `angleCAD = angle DBC = 55°`
`angleDAB = angleCAD + angle BAC `
= 55° + 45 °
= 100°
Since `angleDAB + angle BCD = 180°` (Opposite angle of cyclic quadrilateral)
`angleBCD ` = 180° - 100°
= 80°
Hence `angle BCD = 80°`
APPEARS IN
संबंधित प्रश्न
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

Prove that a cyclic parallelogram is a rectangle.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
