Advertisements
Advertisements
Question
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.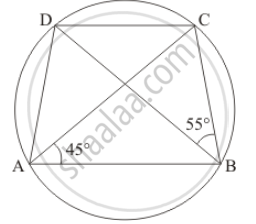
Solution
It is given that ABCD is a cyclic quadrilateral with AC and DB as its diagonals.
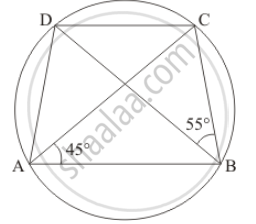
We have to find `angleBCD`
Since angles in the same segment of a circle are equal
So `angleCAD = angle DBC = 55°`
`angleDAB = angleCAD + angle BAC `
= 55° + 45 °
= 100°
Since `angleDAB + angle BCD = 180°` (Opposite angle of cyclic quadrilateral)
`angleBCD ` = 180° - 100°
= 80°
Hence `angle BCD = 80°`
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
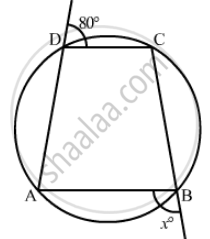
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
