Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
Options
True
False
Solution
This statement is False.
Explanation:
In a cyclic quadrilateral, the sum of opposite angles is 180°.
Now, ∠A + ∠C = 90° + 95° = 185° ≠ 180°
And ∠B + ∠D = 70° + 105° = 175° ≠ 180°
Here, we see that, the sum of opposite angles is not equal to 180°.
So, it is not a cyclic quadrilateral.
APPEARS IN
RELATED QUESTIONS
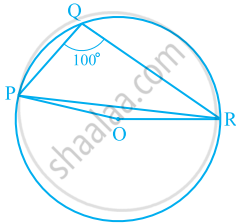
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
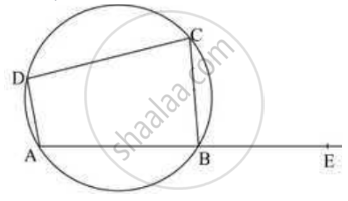
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
