Advertisements
Advertisements
Question
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
Solution
Given: ABCD is a cyclic quadrilateral.
DP and QB are the bisectors of ∠D and ∠B, respectively.
To prove: PQ is the diameter of a circle.
Construction: Join QD and QC.

Proof: Since, ABCD is a cyclic quadrilateral.
∴ ∠CDA + ∠CBA = 180° ...[Sum of opposite angles of cyclic quadrilateral is 180°]
On dividing both sides by 2, we get
`1/2 ∠CDA + 1/2 ∠CBA = 1/2 xx 180^circ = 90^circ`
⇒ ∠1 + ∠2 = 90° ...(i) `[∠1 = 1/2 ∠CDA "and" ∠2 = 1/2 ∠CBA]`
But ∠2 = ∠3 [Angles in the same segment QC are equal] ...(ii)
∠1 + ∠3 = 90°
From equations (i) and (ii),
∠PDQ = 90°
Hence, PQ is a diameter of a circle, because diameter of the circle.
Subtends a right angle at the circumference.
APPEARS IN
RELATED QUESTIONS
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that a cyclic parallelogram is a rectangle.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
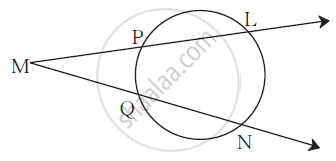
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
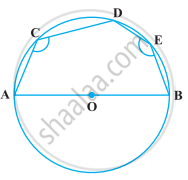
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
