Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
Options
80º
50º
40º
30º
Solution
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to 50º.
Explanation:
Given, ABCD is a cyclic quadrilateral and ∠ADC = 140°.
We know that, sum of the opposite angles in a cyclic quadrilateral is 180°.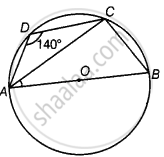
∠ADC + ∠ABC = 180°
⇒ 140° + ∠ABC = 180°
⇒ ∠ABC = 180° – 140°
∴ ∠ABC = 40°
Since, ∠ACB is an angle in a semi-circle.
∴ ∠ACB = 90°
In ΔABC, ∠BAC + ∠ACB + ∠ABC = 180° ...[By angle sum property of a triangle]
⇒ ∠BAC + 90° + 40° = 180°
⇒ ∠BAC = 180° – 130° = 50°
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
