Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
Options
70°
100°
125°
150°
Solution
70°
It is given that ABCD is cyclic quadrilateral ∠ADB = 90° and ∠DCA = 80°. We have to find ∠DAB
We have the following figure regarding the given information
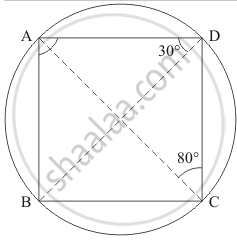
∠BDA = ∠BCA = 30° (Angle in the same segment are equal)
Now, since ABCD is a cyclic quadrilateral
So, ∠DAB + ∠BCD = 180°
`angleDAB + angleBCA + angleDCA` = 180°
`angleDAB ` + 30° + 80° = 180°
`angleDAB` = 180° - 110°
`angleDAB ` = 70 °
APPEARS IN
RELATED QUESTIONS
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that a cyclic parallelogram is a rectangle.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
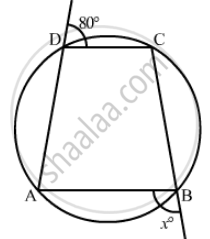
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
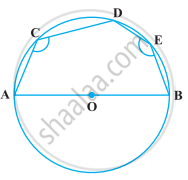
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.