Advertisements
Advertisements
Question
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Options
12 cm
12 cm
12 cm
18 cm
Solution
18 cm
We are given the chord of length 14 cm and perpendicular distance from the centre to the chord is 6 cm. We are asked to find the length of another chord at a distance of 2 cm from the centre.
We have the following figure
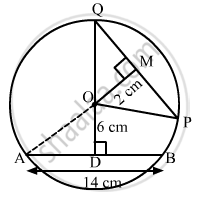
We are given AB = 14 cm, OD = 6 cm, MO = 2 cm, PQ = ?
Since, perpendicular from centre to the chord divide the chord into two equal parts
Therefore
`AQ^2 = AD^2 +OD^2`
= ` 7^2 + 6^2`
= 49 + 36
`= sqrt( 85)`
Now consider the ΔOPQ in which OM = 2 cm
So using Pythagoras Theorem in ΔOPM
`PM^2 = OP^2 -OM^2`
`=(sqrt(85))^2 - 2^2` (∵ OP = AO = radius)
= 81
= 9 cm
Hence PQ = 2 PM
= 2 × 9
= 18 cm
APPEARS IN
RELATED QUESTIONS
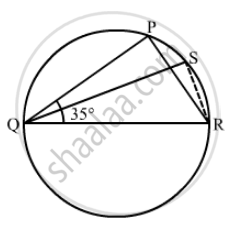
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
If O is the centre of the circle, find the value of x in each of the following figures

Use the figure given below to fill in the blank:
________ is a radius of the circle.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.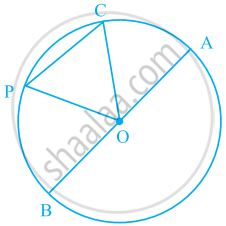
From the figure, identify a point in the exterior.

