Advertisements
Advertisements
Question
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Solution
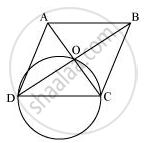
Let ABCD be a rhombus in which diagonals are intersecting at point O and a circle is drawn while taking side CD as its diameter. We know that a diameter subtends 90° on the arc.
∴ ∠COD = 90°
Also, in rhombus, the diagonals intersect each other at 90°.
∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Clearly, point O has to lie on the circle.
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
