Advertisements
Advertisements
प्रश्न
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
उत्तर
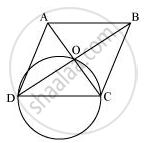
Let ABCD be a rhombus in which diagonals are intersecting at point O and a circle is drawn while taking side CD as its diameter. We know that a diameter subtends 90° on the arc.
∴ ∠COD = 90°
Also, in rhombus, the diagonals intersect each other at 90°.
∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Clearly, point O has to lie on the circle.
APPEARS IN
संबंधित प्रश्न
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
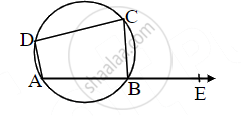
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
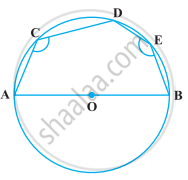
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
