Advertisements
Advertisements
Question
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
Options
41°
23°
67°
18°
Solution
Here we have a cyclic quadrilateral PQRS with PR being a diameter of the circle. Let the centre of this circle be ‘O’.
We are given that `angleQPR` and `angleSPR = 72°` . This is shown in fig (2).
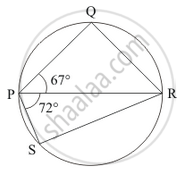
So we see that,
\[\angle QPS = \angle QPR + \angle RPS\]
\[ = 67°+ 72° \]
\[ = 139°\]
In a cyclic quadrilateral it is known that the opposite angles are supplementary.
`angleQPS + angleQRS = 180°`
`angleQRS = 180° - angleQPS`
`= 180° - 139°`
= 41°
APPEARS IN
RELATED QUESTIONS
Prove that a cyclic parallelogram is a rectangle.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
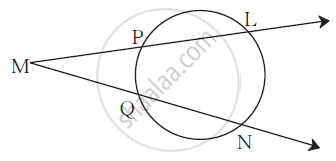
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.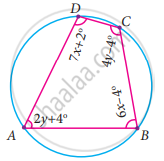
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
