Advertisements
Advertisements
प्रश्न
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
विकल्प
41°
23°
67°
18°
उत्तर
Here we have a cyclic quadrilateral PQRS with PR being a diameter of the circle. Let the centre of this circle be ‘O’.
We are given that `angleQPR` and `angleSPR = 72°` . This is shown in fig (2).
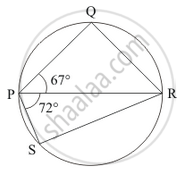
So we see that,
\[\angle QPS = \angle QPR + \angle RPS\]
\[ = 67°+ 72° \]
\[ = 139°\]
In a cyclic quadrilateral it is known that the opposite angles are supplementary.
`angleQPS + angleQRS = 180°`
`angleQRS = 180° - angleQPS`
`= 180° - 139°`
= 41°
APPEARS IN
संबंधित प्रश्न
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
