Advertisements
Advertisements
Question
Find all the angles of the given cyclic quadrilateral ABCD in the figure.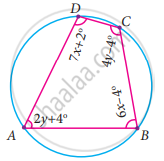
Solution
In a cyclic quadrilateral ABCD,
∠B + ∠D = 180° ...(Sum of the opposite angles of a cyclic quadrilateral is 180°)
6x – 4° + 7x + 2° = 180°
13x – 2° = 180°
13x = 182°
x = 182°
x = `(182^circ)/13`
x = 14°
∠B = 6x – 4°
= 6(14) – 4°
= 84 – 4
= 80°
∠D = 7x + 2°
= 7(14) + 2°
= 98 + 2
= 100°
2y + 4° + 4y – 4° = 180° ...(Sum of the opposite angles of a cyclic quadrilateral is 180°)
6y = 180°
y = `(180^circ)/6`
= 30°
∠A = 2y + 4°
= 2(30) + 4°
= 64°
∠C = 4y – 4°
= 4(30) – 4°
= 120° – 4°
= 116°
∴ ∠A = 64°, ∠B = 80°, ∠C = 116°, ∠D = 100°.
APPEARS IN
RELATED QUESTIONS
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
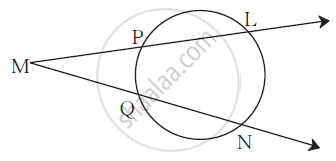
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
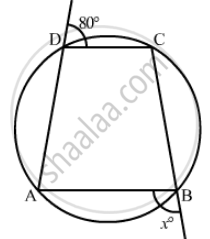
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.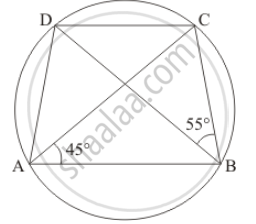
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
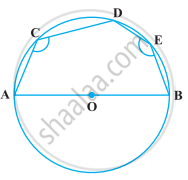
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.