Advertisements
Advertisements
प्रश्न
Find all the angles of the given cyclic quadrilateral ABCD in the figure.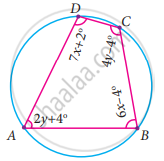
उत्तर
In a cyclic quadrilateral ABCD,
∠B + ∠D = 180° ...(Sum of the opposite angles of a cyclic quadrilateral is 180°)
6x – 4° + 7x + 2° = 180°
13x – 2° = 180°
13x = 182°
x = 182°
x = `(182^circ)/13`
x = 14°
∠B = 6x – 4°
= 6(14) – 4°
= 84 – 4
= 80°
∠D = 7x + 2°
= 7(14) + 2°
= 98 + 2
= 100°
2y + 4° + 4y – 4° = 180° ...(Sum of the opposite angles of a cyclic quadrilateral is 180°)
6y = 180°
y = `(180^circ)/6`
= 30°
∠A = 2y + 4°
= 2(30) + 4°
= 64°
∠C = 4y – 4°
= 4(30) – 4°
= 120° – 4°
= 116°
∴ ∠A = 64°, ∠B = 80°, ∠C = 116°, ∠D = 100°.
APPEARS IN
संबंधित प्रश्न
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
