Advertisements
Chapters
![Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 4 - Geometry Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 4 - Geometry - Shaalaa.com](/images/mathematics-english-class-9-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 4: Geometry
Below listed, you can find solutions for Chapter 4 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Mathematics [English] Class 9 TN Board.
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.1 [Pages 143 - 144]
In the figure, AB is parallel to CD, find x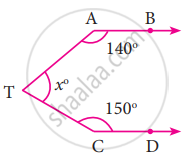
In the figure, AB is parallel to CD, find x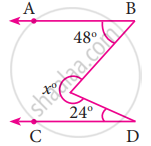
In the figure, AB is parallel to CD, find x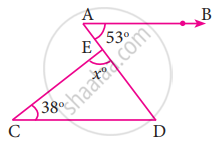
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: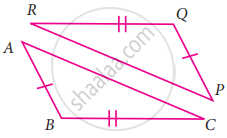
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: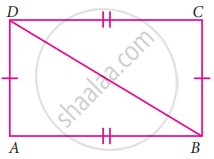
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: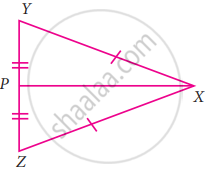
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: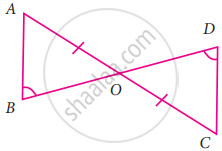
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: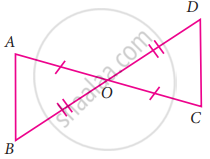
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: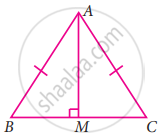
ΔABC and ΔDEF are two triangles in which AB = DF, ∠ACB = 70°, ∠ABC = 60°, ∠DEF = 70° and ∠EDF = 60°. Prove that the triangles are congruent
Find all the three angles of the ΔABC
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.2 [Pages 157 - 158]
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus
Show that the bisectors of angles of a parallelogram form a rectangle
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between b and c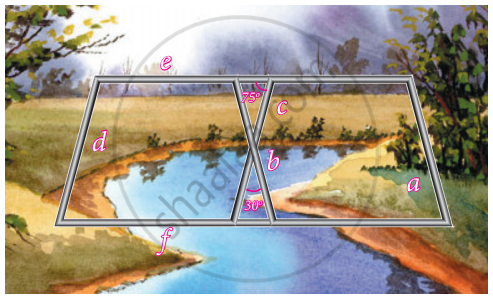
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e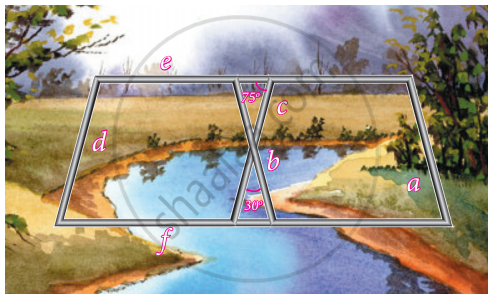
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and f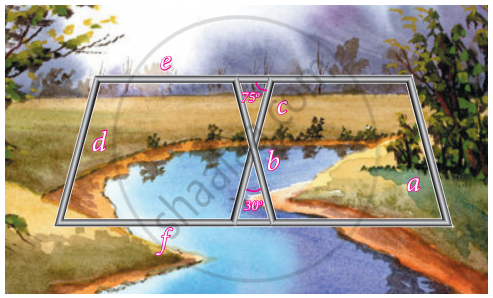
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between c and f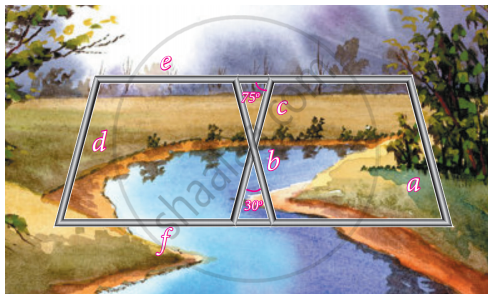
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°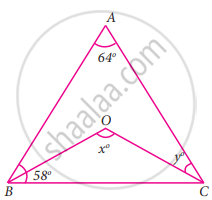
In the given Figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF. (Use congruent property of triangles)
In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD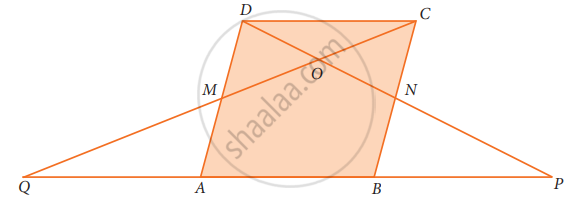
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.3 [Pages 169 - 170]
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
Find the value of x° in the following figure: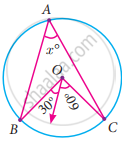
Find the value of x° in the following figure: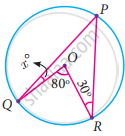
Find the value of x° in the following figure: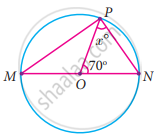
Find the value of x° in the following figure: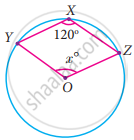
Find the value of x° in the following figure: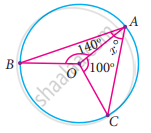
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.4 [Pages 173 - 174]
Find the value of x in the given figure.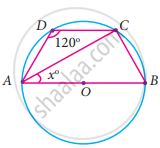
In the given figure, AC is the diameter of the circle with centre O. If ∠ADE = 30°, ∠DAC = 35° and ∠CAB = 40°. Find ∠ACD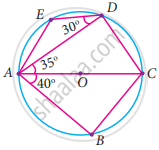
In the given figure, AC is the diameter of the circle with centre O. If ∠ADE = 30°, ∠DAC = 35° and ∠CAB = 40°. Find ∠ACB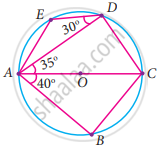
In the given figure, AC is the diameter of the circle with centre O. If ∠ADE = 30°, ∠DAC = 35° and ∠CAB = 40°. Find ∠DAE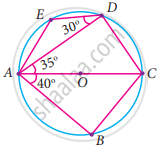
Find all the angles of the given cyclic quadrilateral ABCD in the figure.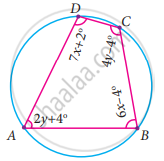
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find ∠CAD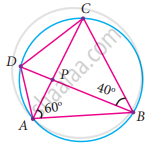
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find ∠BCD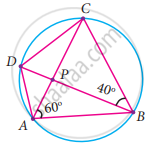
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8 cm and CD = 6 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7cm. Find the radius of the circle?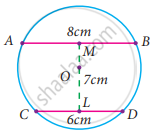
The arch of a bridge has dimensions as shown, where the arch measure 2m at its highest point and its width is 6m. What is the radius of the circle that contains the arch?
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6 m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8 m, CD = 10 m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.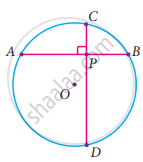
In the given figure, ∠POQ = 100° and ∠PQR° = 30°, then find ∠RPO
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.5 [Page 177]
Construct the ΔLMN such that LM = 7.5 cm, MN = 5 cm and LN = 8 cm. Locate its centroid
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4 cm and AC = 3 cm
Draw the ΔABC, where AB = 6 cm, ∠B = 110° and AC = 9 cm and construct the centroid
Construct the ΔPQR such that PQ = 5 cm, PR = 6 cm and ∠QPR = 60° and locate its centroid
Draw ΔPQR with sides PQ = 7 cm, QR = 8 cm and PR = 5 cm and construct its Orthocentre
Draw an equilateral triangle of sides 6.5 cm and locate its Orthocentre
Draw ΔABC, where AB = 6 cm, ∠B = 110° and BC = 5 cm and construct its Orthocentre
Draw and locate the Orthocentre of a right triangle PQR where PQ = 4.5 cm, QR = 6 cm and PR = 7.5 cm
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.6 [Pages 180 - 181]
Draw a triangle ABC, where AB = 8 cm, BC = 6 cm and ∠B = 70° and locate its circumcentre and draw the circumcircle
Construct the right triangle PQR whose perpendicular sides are 4.5 cm and 6 cm. Also locate its circumcentre and draw circumcircle
Construct ΔABC with AB = 5 cm ∠B = 100° and BC = 6 cm. Also locate its circumcentre draw circumcircle
Construct an isosceles triangle PQR where PQ = PR and ∠Q = 50°, QR = 7 cm. Also draw its circumcircle.
Draw an equilateral triangle of side 6.5 cm and locate its incentre. Also draw the incircle
Draw a right triangle whose hypotenuse is 10 cm and one of the legs is 8 cm. Locate its incentre and also draw the incircle
Draw ΔABC given AB = 9 cm, ∠CAB = 115° and ∠ABC = 40°. Locate its incentre and also draw the incircle.
Construct ΔABC in which AB = BC = 6 cm and ∠B = 80°. Locate its incentre and draw the incircle
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 4 Geometry Exercise 4.7 [Pages 181 - 183]
Multiple Choice Questions
The exterior angle of a triangle is equal to the sum of two
Exterior angles
Interior opposite angles
Alternate angles
Interior angles
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is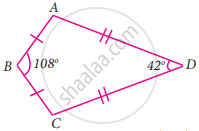
150°
30°
105°
72°
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are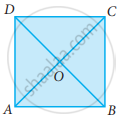
6
8
4
12
In the given figure CE || DB then the value of x° is
45°
30°
75°
85°
The correct statement out of the following is 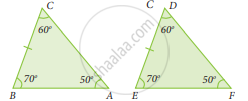
ΔABC ≅ ΔDEF
ΔABC ≅ ΔEDF
ΔABC ≅ ΔFDE
ΔABC ≅ ΔFED
If the diagonal of a rhombus are equal, then the rhombus is a
Parallelogram but not a rectangle
Rectangle but not a square
Square
Parallelogram but not a square
If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is
∠C + ∠D
`1/2 (∠"C" + ∠"D")`
`1/2 ∠"C" + 1/3 ∠"D"`
`1/3 ∠"C" + 1/2 ∠"D"`
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
rhombus
rectangle
trapezium
kite
Which of the following statement is correct?
Opposite angles of a parallelogram are not equal.
Adjacent angles of a parallelogram are complementary.
Diagonals of a parallelogram are always equal.
Both pairs of opposite sides of a parallelogram are always equal.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
40°
35°
50°
45°
PQ and RS are two equal chords of a circle with centre O such that ∠POQ = 70°, then ∠ORS =
60°
70°
55°
80°
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
25 cm
20 cm
40 cm
18 cm
In the figure, O is the centre of the circle and ∠ACB = 40° then ∠AOB =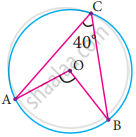
80°
85°
70°
65°
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
30°
20°
15°
25°
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is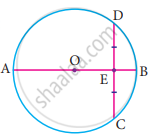
8 cm
4 cm
6 cm
10 cm
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 100°, then ∠TVS =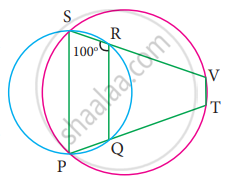
80°
100°
70°
90°
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
100°
105°
85°
90°
In the figure, ABCD is a cyclic quadrilateral in which DC produced to E and CF is drawn parallel to AB such that ∠ADC = 80° and ∠ECF = 20°, then BAD =?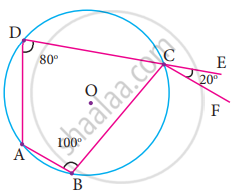
100°
20°
120°
110°
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
10 cm
9 cm
8 cm
6 cm
In the given figure, If OP = 17 cm, PQ = 30 cm and OS is perpendicular to PQ, then RS is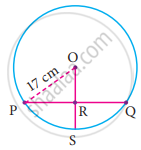
10 cm
6 cm
7 cm
9 cm
Solutions for 4: Geometry
![Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 4 - Geometry Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 4 - Geometry - Shaalaa.com](/images/mathematics-english-class-9-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 4 - Geometry
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Mathematics [English] Class 9 TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Mathematics [English] Class 9 TN Board Tamil Nadu Board of Secondary Education 4 (Geometry) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 TN Board chapter 4 Geometry are Types of Angles, Related Angles, Complementary Angles, Supplementary Angles, Concept of Linear Pair, Concept of Vertically Opposite Angles, Concept of Angle, Pairs of Lines - Transversal, Pairs of Lines - Angles Made by a Transversal, Pairs of Lines - Transversal of Parallel Lines, Concept of Triangles, Criteria for Congruence of Triangles, SSS Congruence Criterion, SAS Congruence Criterion, ASA Congruence Criterion, RHS Congruence Criterion, Concept of Quadrilaterals, Types of Quadrilaterals, Properties of a Square, Properties of Rectangle, Properties of a Parallelogram, Properties of Rhombus, Properties of Trapezium, Properties of Isosceles Trapezium, Properties of Kite, Theorem: In a Parallelogram, Opposite Sides Are Equal., Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles., Property: The Opposite Sides of a Parallelogram Are of Equal Length., Angle Subtended by Chord at the Centre, Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection), Theorem: Parallelograms on the Same Base and Between the Same Parallels., Corollary: Triangles on the same base and between the same parallels are equal in area., Corollary: A rectangle and a parallelogram on the same base and between the same parallels are equal in area., Concept of Circle, Congruence of Circles, Circles Passing Through One, Two, Three Points, Perpendicular from the Centre to a Chord, Theorem: a Perpendicular Drawn from the Centre of a Circle on Its Chord Bisects the Chord., Converse: The Line Joining the Centre of the Circle and the Midpoint of a Chord is Perpendicular to the Chord., Theorem: Equal chords of a circle subtend equal angles at the centre., Converse: If the angles subtended by two chords at the centre of a circle are equal, then the chords are equal., Theorem: Equal chords of a circle are equidistant from the centre., Theorem : The Chords of a Circle Which Are Equidistant from the Centre Are Equal., Angle Subtended by an Arc of a Circle, Angle at the Centre and the Circumference, Theorem: The angle subtended by an arc of the circle at the centre is double the angle subtended by it at any point on the remaining part of the circle., Theorem: Angles in the Same Segment of a Circle Are Equal., Cyclic Quadrilateral, Theorem: Opposite angles of a cyclic quadrilateral are supplementary., Converse: If a Pair of Opposite Angles of a Quadrilateral is Supplementary, Then the Quadrilateral is Cyclic., Exterior Angle of a Cyclic Quadrilateral, Theorem: If One Side of a Cyclic Quadrilateral is Produced Then the Exterior Angle is Equal to the Interior Opposite Angle., Construction of the Centroid of a Triangle., Construction of Orthocentre of a Triangle, Construction of the Circumcentre of a Triangle, Construction of the Incircle of a Triangle., Concept for Angle Sum Property.
Using Samacheer Kalvi Mathematics [English] Class 9 TN Board solutions Geometry exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Mathematics [English] Class 9 TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 4, Geometry Mathematics [English] Class 9 TN Board additional questions for Mathematics Mathematics [English] Class 9 TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.
