Advertisements
Advertisements
प्रश्न
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8 cm and CD = 6 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7cm. Find the radius of the circle?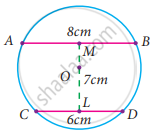
उत्तर
Let OM be x.
∴ OL = 7 – x
In the right ΔAOM,
OA2 = AM2 + OM2
= 42 + x2
OA2 = 16 + x2
r2 = 16 + x2 ...(1) [r is the radius]
In the right ΔOCL,
OC2 = OL2 + CL2
r2 = (7 – x)2 + 32
= 49 + x2 – 14x + 9
= 58 + x2 – 14x …….. (2)
From (1) and (2) we get,
16 + x2 = 58 + x2 – 14x
14x = 58 – 16
14x = 42
x = `42/14`
x = 3 cm
r2 = 16 + x2
= 16 + 9
= 25
∴ r = `sqrt(25)`
= 5
∴ radius of the circle = 5 cm.
APPEARS IN
संबंधित प्रश्न
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find ∠CAD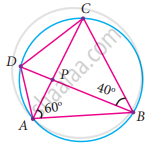
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find ∠BCD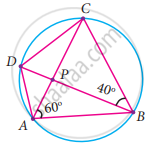
The arch of a bridge has dimensions as shown, where the arch measure 2m at its highest point and its width is 6m. What is the radius of the circle that contains the arch?
In the given figure, ∠POQ = 100° and ∠PQR° = 30°, then find ∠RPO
