Advertisements
Advertisements
प्रश्न
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
विकल्प
30°
20°
15°
25°
उत्तर
30°
Explanation;
Hint:
∠A + ∠C = 180° ...(Sum of the opposite angle of cyclic quadrilateral is 180°)
4x + 2x = 180°
x = `(180^circ)/6`
= 30°
APPEARS IN
संबंधित प्रश्न
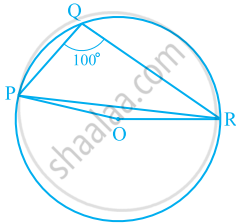
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
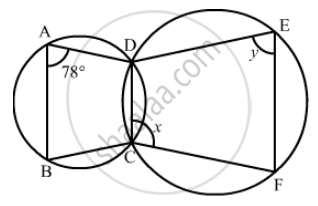
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.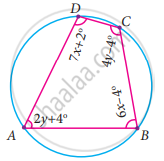
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
