Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
उत्तर
EB = EC
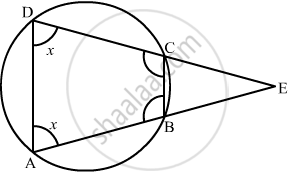
Since, AD and BC are parallel to each other, so,
\[\angle ECB = \angle EDA \left( \text{ Corresponding angles } \right)\]
\[\angle EBC = \angle EAD \left( \text{ Corresponding angles} \right)\]
\[\text{ But } , \angle EDA = \angle EAD\]
\[\text{ Therefore } , \angle ECB = \angle EBC\]
\[ \Rightarrow EC = EB\]
\[ \text{ Therefore, } \bigtriangleup \text{ ECB is an isosceles triangle } .\]
APPEARS IN
संबंधित प्रश्न
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
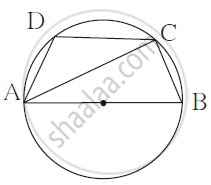
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
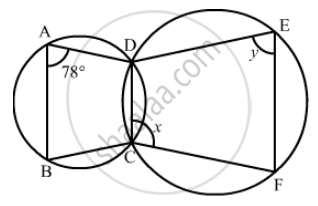
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
