Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
Advertisements
उत्तर
EB = EC
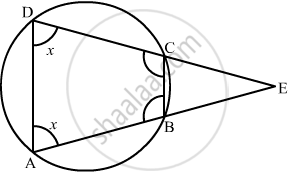
Since, AD and BC are parallel to each other, so,
\[\angle ECB = \angle EDA \left( \text{ Corresponding angles } \right)\]
\[\angle EBC = \angle EAD \left( \text{ Corresponding angles} \right)\]
\[\text{ But } , \angle EDA = \angle EAD\]
\[\text{ Therefore } , \angle ECB = \angle EBC\]
\[ \Rightarrow EC = EB\]
\[ \text{ Therefore, } \bigtriangleup \text{ ECB is an isosceles triangle } .\]
APPEARS IN
संबंधित प्रश्न
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90°-A, 90° − `1/2 A, 90° − 1/2 B, 90° − 1/2` C.
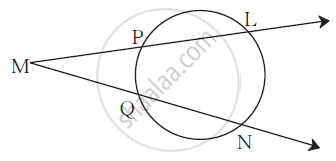
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.
ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
