Advertisements
Advertisements
प्रश्न
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
उत्तर
Given:- □ABCD is a cyclic quadrilateral.
To prove:- ∠BAD + ∠BCD = 180º and ∠ABC + ∠ADC = 180º
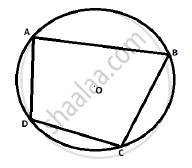
Proof:- Arc BCD is intercepted by the inscribed ∠BAD.
∠BAD = `1/2` m(arc BCD) ..........(i) [Inscribed angle theorem]
Arc BAD is intercepted by the inscribed ∠BCD.
∴ ∠BCD = `1/2` m(arc DAB) ..........(ii) [Inscribed angle theorem]
From (1) and (2) we get
∠BAD + ∠BCD = `1/2` [m(arc BCD) + m(arc DAB)]
∴ (∠BAD + ∠BCD) = `1/2 xx 360^circ` .....[Completed circle]
= 180°
Again, as the sum of the measures of angles of a quadrilateral is 360°
∴ ∠ADC + ∠ABC = 360° – [∠BAD + ∠BCD]
= 360° – 180°
= 180°
Hence the opposite angles of a cyclic quadrilateral are supplementary.
APPEARS IN
संबंधित प्रश्न
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
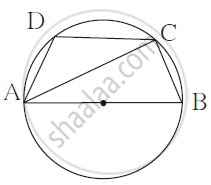
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
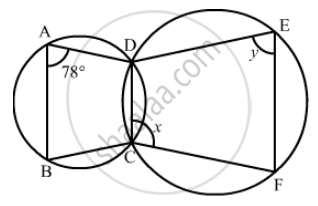
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.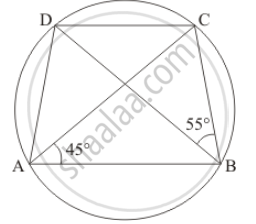
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
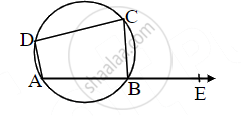
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
