Advertisements
Advertisements
प्रश्न
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
उत्तर

In ΔAOD and ΔCOE,
OA = OC (Radii of the same circle)
OD = OE (Radii of the same circle)
AD = CE (Given)
∴ ΔAOD ≅ ΔCOE (SSS congruence rule)
∠OAD = ∠OCE (By CPCT) ... (1)
∠ODA = ∠OEC (By CPCT) ... (2)
Also,
∠OAD = ∠ODA (As OA = OD) ... (3)
From equations (1), (2), and (3), we obtain
∠OAD = ∠OCE = ∠ODA = ∠OEC
Let ∠OAD = ∠OCE = ∠ODA = ∠OEC = x
In Δ OAC,
OA = OC
∴ ∠OCA = ∠OAC (Let a)
In Δ ODE,
OD = OE
∠OED = ∠ODE (Let y)
ADEC is a cyclic quadrilateral.
∴ ∠CAD + ∠DEC = 180° (Opposite angles are supplementary)
x + a + x + y = 180°
2x + a + y = 180°
y = 180º − 2x − a ... (4)
However, ∠DOE = 180º − 2y
And, ∠AOC = 180º − 2a
∠DOE − ∠AOC = 2a − 2y = 2a − 2 (180º − 2x − a)
= 4a + 4x − 360° ... (5)
∠BAC + ∠CAD = 180º (Linear pair)
⇒ ∠BAC = 180º − ∠CAD = 180º − (a + x)
Similarly, ∠ACB = 180º − (a + x)
In ΔABC,
∠ABC + ∠BAC + ∠ACB = 180º (Angle sum property of a triangle)
∠ABC = 180º − ∠BAC − ∠ACB
= 180º − (180º − a − x) − (180º − a −x)
= 2a + 2x − 180º
= 1/2[4a + 4x − 360°]
∠ABC = 1/2[∠DOE − ∠ AOC] [Using equation (5)]
APPEARS IN
संबंधित प्रश्न
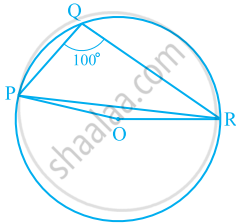
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
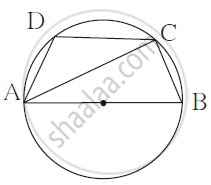
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
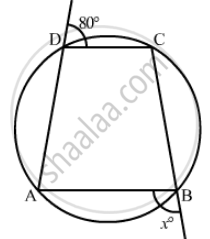
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
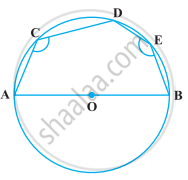
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
