Advertisements
Advertisements
प्रश्न
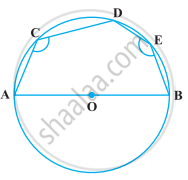
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
उत्तर
Since, A, C, D and E are four point on a circle, then ACDE is a cyclic quadrilateral.
∠ACD + ∠AED = 180° ...(i) [Sum of opposite angles in a cyclic quadrilateral is 180°]
Now, ∠AEB = 90° ...(ii)
We know that, diameter subtends a right angle to the circle.
On adding equations (i) and (ii), we get
(∠ACD + ∠AED) + ∠AEB = 180° + 90° = 270°
⇒ ∠ACD + ∠BED = 270°
APPEARS IN
संबंधित प्रश्न
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
Prove that a cyclic parallelogram is a rectangle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
