Advertisements
Advertisements
प्रश्न
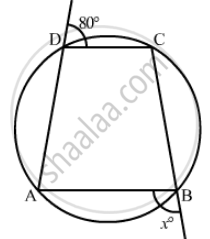
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
उत्तर
Here, ABCD is a cyclic quadrilateral, we need to find x.
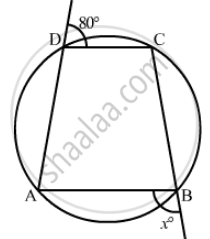
In cyclic quadrilateral the sum of opposite angles is equal to 180°.
Therefore,
Hence, the value of x is 100°.
APPEARS IN
संबंधित प्रश्न
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
In the figure,
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
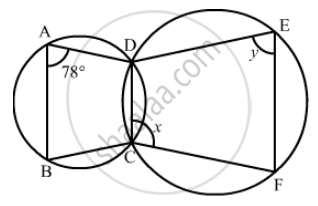
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.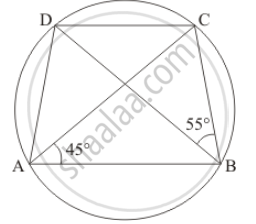
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
