Advertisements
Advertisements
प्रश्न
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
उत्तर
Given: ABCD is a cyclic quadrilateral.
DP and QB are the bisectors of ∠D and ∠B, respectively.
To prove: PQ is the diameter of a circle.
Construction: Join QD and QC.

Proof: Since, ABCD is a cyclic quadrilateral.
∴ ∠CDA + ∠CBA = 180° ...[Sum of opposite angles of cyclic quadrilateral is 180°]
On dividing both sides by 2, we get
`1/2 ∠CDA + 1/2 ∠CBA = 1/2 xx 180^circ = 90^circ`
⇒ ∠1 + ∠2 = 90° ...(i) `[∠1 = 1/2 ∠CDA "and" ∠2 = 1/2 ∠CBA]`
But ∠2 = ∠3 [Angles in the same segment QC are equal] ...(ii)
∠1 + ∠3 = 90°
From equations (i) and (ii),
∠PDQ = 90°
Hence, PQ is a diameter of a circle, because diameter of the circle.
Subtends a right angle at the circumference.
APPEARS IN
संबंधित प्रश्न
Prove that a cyclic parallelogram is a rectangle.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
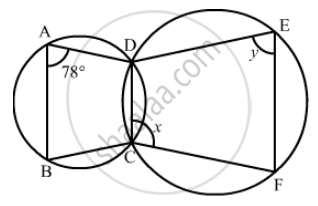
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
