Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
उत्तर
It is given that BC || AD , `angleADC = 110°` and `angleBAC = 50°`
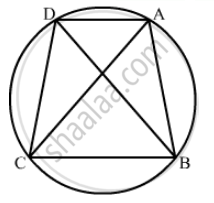
We have to find `angleDAC`
In cyclic quadrilateral ABCD
`angleA + angleC = 180°` ..… (1)
`angleB + angleD = 180°` ..… (2)
Since, `angleADC = 110°`
So,
`angleB = 180° - angleD`
`=180° - 110°`
= 70°
Therefore in Δ ABC , 50° + 70° + ` angle BCA `= 180°
So , `angleBCA` = 60° ..… (3)
Now, `angleBCA = angle CAD ` (BC || AD and AC is transversal)
`⇒ angle BCA = angle CAD` = 60°
APPEARS IN
संबंधित प्रश्न
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
