Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
उत्तर
It is given that BC || AD , `angleADC = 110°` and `angleBAC = 50°`
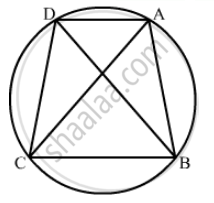
We have to find `angleDAC`
In cyclic quadrilateral ABCD
`angleA + angleC = 180°` ..… (1)
`angleB + angleD = 180°` ..… (2)
Since, `angleADC = 110°`
So,
`angleB = 180° - angleD`
`=180° - 110°`
= 70°
Therefore in Δ ABC , 50° + 70° + ` angle BCA `= 180°
So , `angleBCA` = 60° ..… (3)
Now, `angleBCA = angle CAD ` (BC || AD and AC is transversal)
`⇒ angle BCA = angle CAD` = 60°
APPEARS IN
संबंधित प्रश्न
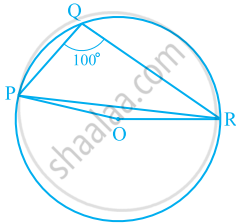
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
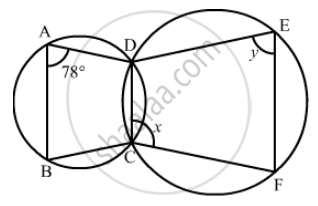
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
