Advertisements
Advertisements
प्रश्न
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
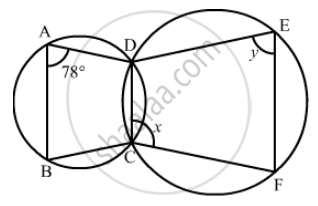
उत्तर
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
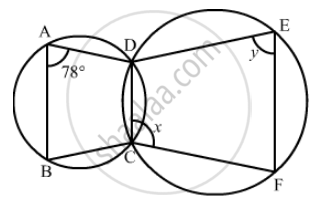
We have to find the value of x and y.
Since ,ABCD is a cyclic quadrilateral
So `angle A + angle BCD = 180°` (Opposite angle of a cyclic quadrilateral are supplementary)
` angle BCD = 180° - angle A ` ` ( ∠ A = 78°)`
`angle BCD = 180° - 78°`
`angle BCD = 102°` ..… (1)
`angle BCD + angleDCF = 180°`
`DCF = 180° - angle BCD `
x = 180° − 102°
= 78°
Now in cyclic quadrilateral DCFE
x + y = 180° (Opposite angles of a cyclic quadrilateral are supplementary)
y = 180° − 78°
= 102°
Hence, x = 78° and y = 102°
APPEARS IN
संबंधित प्रश्न
Prove that a cyclic parallelogram is a rectangle.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
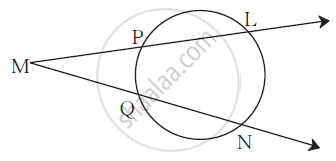
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.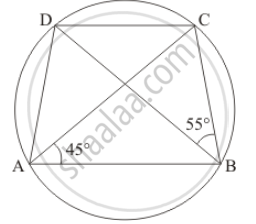
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
