Advertisements
Advertisements
Question
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
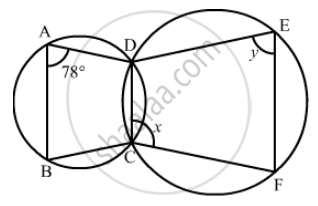
Solution
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
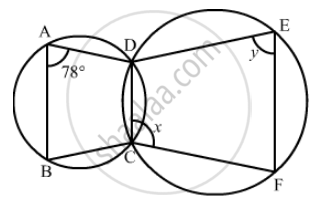
We have to find the value of x and y.
Since ,ABCD is a cyclic quadrilateral
So `angle A + angle BCD = 180°` (Opposite angle of a cyclic quadrilateral are supplementary)
` angle BCD = 180° - angle A ` ` ( ∠ A = 78°)`
`angle BCD = 180° - 78°`
`angle BCD = 102°` ..… (1)
`angle BCD + angleDCF = 180°`
`DCF = 180° - angle BCD `
x = 180° − 102°
= 78°
Now in cyclic quadrilateral DCFE
x + y = 180° (Opposite angles of a cyclic quadrilateral are supplementary)
y = 180° − 78°
= 102°
Hence, x = 78° and y = 102°
APPEARS IN
RELATED QUESTIONS
Prove that a cyclic parallelogram is a rectangle.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
