Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
उत्तर
Given: ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawn that it intersect AD at P and BC at Q.
To prove: Points P, Q, C and D are con-cyclic.
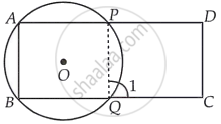
Construction: Join PQ
Proof: ∠1 = ∠A ...[Exterior angle property of cyclic quadrilateral]
But ∠A = ∠C ...[Opposite angles of a parallelogram]
∴ ∠1 = ∠C ...(i)
But ∠C + ∠D = 180° ...[Sum of cointerior angles on same side is 180°]
⇒ ∠1 + ∠D = 180° ...[From equation (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q, C and D are con-cyclic.
Hence proved.
APPEARS IN
संबंधित प्रश्न
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
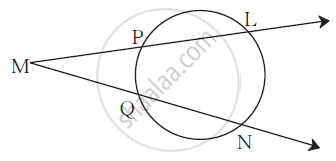
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
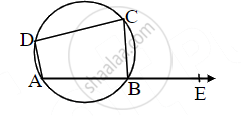
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
