Advertisements
Advertisements
प्रश्न
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
उत्तर
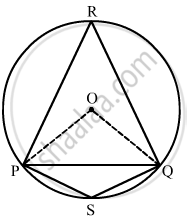
\[ \stackrel\frown{QP} \text{ is a major arc and } \angle PSQ \text{ is the angle formed by it in the alternate segment } . \]
\[ \text{ We know that the angle subtended by an arc at the centre is twice the angle subtended by it at any point of the alternate segment of the circle } . \]
`=> 2angle "PSQ" = "m"`
`=> 2angle "PSQ" = 360^circ - "m"`
`=> 2 angle"PSQ" = 360^circ - 180^circ ...(because angle "POQ" < 108^circ)`
`=> 2angle "PSQ" > 180^circ`
`=> angle "PSQ" > 90^circ`
Thus, the angle in a segment shorter than a semi-circle is greater than a right angle.
APPEARS IN
संबंधित प्रश्न
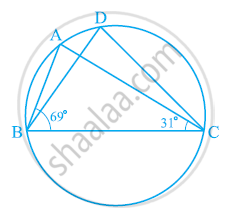
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
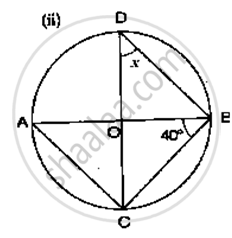
If O is the centre of the circle, find the value of x in the following figure:
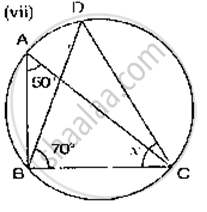
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
