Advertisements
Advertisements
प्रश्न
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
उत्तर
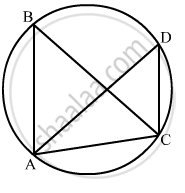
\[\text{ To prove } : \angle ABC \text{ is an acute angle } \]
\[\text{ Proof } : \]
\[\text{ AD being the diameter of the given circle } \]
\[ \Rightarrow \angle ACD = 90° \left[ \text{ Angle in a semicircle is a right angle } \right]\]
\[\text{ Now, in } \bigtriangleup ACD, \angle ACD = 90° \text{ which means that } \angle ADC \text{ is an acute angle } . . . . . . \left( 1 \right)\]
\[\text{ Again, } \angle ABC = \angle ADC \left[ \text{ Angle in a same segment are always equal } \right]\]
\[ \Rightarrow \angle ABC \text{ is also an acute angle } . \left[ \text{ Using } \left( 1 \right) \right]\]
\[\text{ Hence proved } \]
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
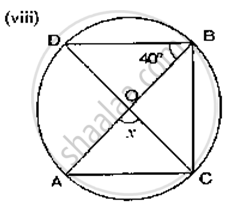
If O is the centre of the circle, find the value of x in the following figure
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
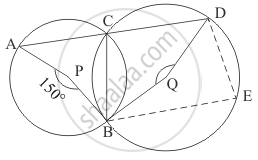
In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

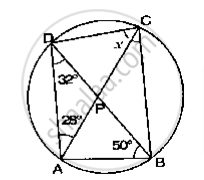
In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =