Advertisements
Advertisements
प्रश्न
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
उत्तर
Here, ABCD is a cyclic rectangle; we have to prove that the centre of the corresponding circle is the intersection of its diagonals.
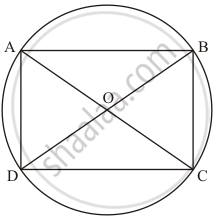
Let O be the centre of the circle.
We know that the angle formed in the semicircle is 90°.
Since, ABCD is a rectangle, So
`angleADC = angleDCB = angleABC = angleBAD = 90°`
Therefore, AC and BD are diameter of the circle.
We also know that the intersection of any two diameter is the centre of the circle.
Hence, the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
APPEARS IN
संबंधित प्रश्न
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that a cyclic parallelogram is a rectangle.
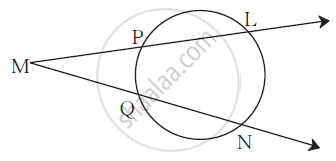
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
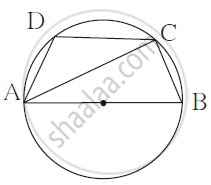
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
