Advertisements
Advertisements
प्रश्न
In the figure, AB is parallel to CD, find x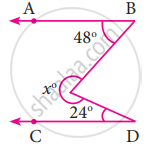
उत्तर
Draw TE || AB.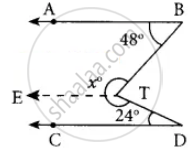
∠ABT + ∠ETB = 180° ...(AB || TE)
48° + ∠ETB = 180°
∠ETB = 180° – 48° = 132°
Similarly ∠CDT + ∠DTE = 180°
24° + ∠DTE = 180°
∴ ∠DTE = 180° – 24°
= 156°
∴ ∠BTE + ∠ETD = 132° + 156°
= 288°
x = 288°
APPEARS IN
संबंधित प्रश्न
Find the unknown angles in the given figure:
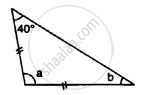
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
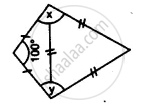
Find the unknown angles in the given figure:
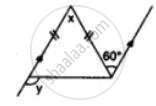
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
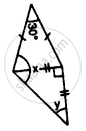
In an isosceles triangle, each base angle is four times its vertical angle. Find all the angles of the triangle.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
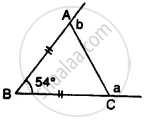
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.
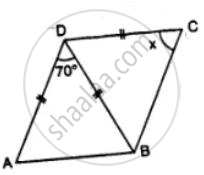
Find x in Figure Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠ABE

