Advertisements
Advertisements
प्रश्न
In the figure, AB is parallel to CD, find x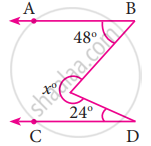
उत्तर
Draw TE || AB.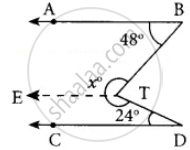
∠ABT + ∠ETB = 180° ...(AB || TE)
48° + ∠ETB = 180°
∠ETB = 180° – 48° = 132°
Similarly ∠CDT + ∠DTE = 180°
24° + ∠DTE = 180°
∴ ∠DTE = 180° – 24°
= 156°
∴ ∠BTE + ∠ETD = 132° + 156°
= 288°
x = 288°
APPEARS IN
संबंधित प्रश्न
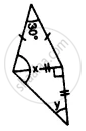
Find the unknown angles in the given figure:
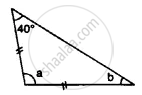
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
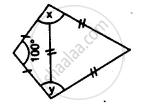
Find the unknown angles in the given figure:
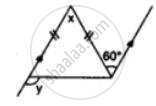
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
In an isosceles triangle, each base angle is four times its vertical angle. Find all the angles of the triangle.
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
In the given figure, BI is the bisector of ∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.
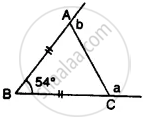
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠BAE