Advertisements
Advertisements
प्रश्न
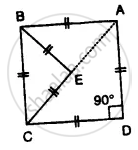
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
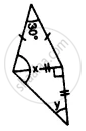
उत्तर
In fig.,
x = a + b
But b = y ..........(Angles opposite to equal sides)
Similarly a = c
But a + c + 30° = 180°
⇒ a + a + 30° = 180°
⇒ 2a + 30° = 180°
⇒ 2a = 180° − 30° = 150°
⇒ a =`(150°)/2=75°` and b + y = 90°
⇒ y + y = 90°
⇒ 2y = 90°
⇒ y =`(90°)/2=45°` ⇒ b = 45°
Hence x = a + b = 75° + 45° = 120° and y = 45°
APPEARS IN
संबंधित प्रश्न
Find the unknown angles in the given figure:
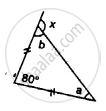
Find the unknown angles in the given figure:
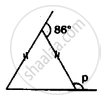
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
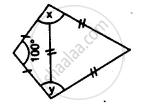
In an isosceles triangle, each base angle is four times its vertical angle. Find all the angles of the triangle.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠BAE
In the figure, AB is parallel to CD, find x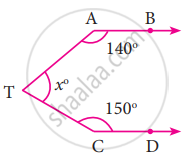
In the figure, AB is parallel to CD, find x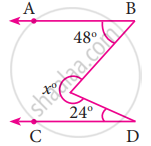
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle
