Advertisements
Advertisements
प्रश्न
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°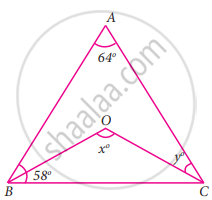
उत्तर
In the given ΔABC
∠A = 64° and ∠B = 58°
∠C = 180° − (64° + 58°)
= 180° – 122°
= 58°
Since OC is the bisector of ∠C
y = `(58^circ)/2`
= 29°
Given ΔOBC
∠OCB = `(58^circ)/2` = 29°
∠OCB = 29°
∴ ∠BOC = 180° − (29° + 29°)
x = 180° – 58°
x = 122°
∠x = 122° and ∠y = 29°.
APPEARS IN
संबंधित प्रश्न
In a parallelogram ABCD, determine the sum of angles ∠C and ∠D .
ABCD is a square. AC and BD intersect at O. State the measure of ∠AOB.
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
We get a rhombus by joining the mid-points of the sides of a
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are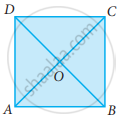
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
