Advertisements
Advertisements
प्रश्न
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a
विकल्प
rectangle
parallelogram
rhombus
square
उत्तर
It is given a parallelogram ABCD in which P,Q,R and S are the mid-points AB, BC, CDand DA respectively.
PQ, QR, RS and SP are joined.
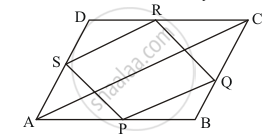
In ΔABC, P and Q are the mid-points AB and BC respectively.
Therefore,
PQ || AC and `PQ = 1/2 AC `……(i)
Similarly, In ΔADC, R and S are the mid-points CD and AD respectively.
Therefore,
SR || AC and `PQ = 1/2 AC ` ……(ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
Therefore, PQRS is a parallelogram.
Hence the correct choice is (b).
APPEARS IN
संबंधित प्रश्न
In a parallelogram ABCD, determine the sum of angles ∠C and ∠D .
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
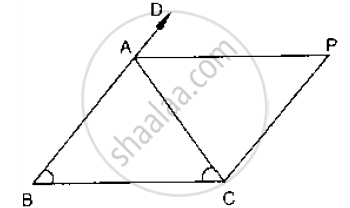
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
We get a rhombus by joining the mid-points of the sides of a
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°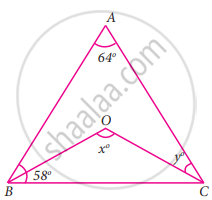
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
