Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, determine the sum of angles ∠C and ∠D .
उत्तर
`∠`C and `∠`D are consecutive interior angles on the same side of the transversal CD
∴`∠`C + `∠`D = 180°
APPEARS IN
संबंधित प्रश्न
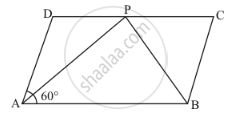
In Fig., below, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
We get a rhombus by joining the mid-points of the sides of a
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
In a quadrilateral ABCD, ∠A + ∠C is 2 times ∠B + ∠D. If ∠A = 140° and ∠D = 60°, then ∠B=
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
