Advertisements
Advertisements
प्रश्न
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
उत्तर
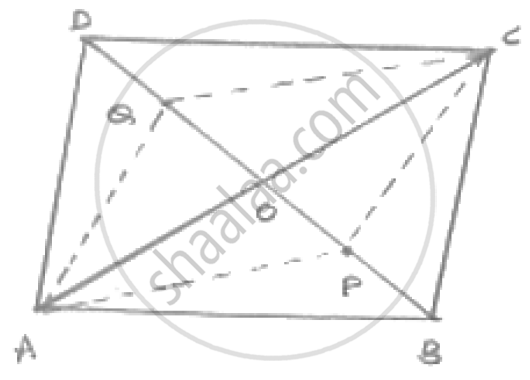
We know that, diagonals of a parallelogram bisect each other
∴OA = OC and OB = OD
Since P and Q are point of intersection of BD
∴BP = PQ = QD
Now, OB = OD and BP = QD
⇒ OB - BP = OD - QD
⇒ OP = OQ
Thus in quadrilateral APCQ, we have
OA = OC and OP = OQ
⇒ diagonals of quadrilateral APCQ bisect each other
∴APCQ is a parallelogram
Hence AP || CQ
APPEARS IN
संबंधित प्रश्न
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following case, PQRS is a parallelogram?
∠P = 100°, ∠Q = 80°, ∠R = 95°
We get a rhombus by joining the mid-points of the sides of a
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
In a quadrilateral ABCD, ∠A + ∠C is 2 times ∠B + ∠D. If ∠A = 140° and ∠D = 60°, then ∠B=
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
