Advertisements
Advertisements
प्रश्न
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
विकल्प
square
rectangle
trapezium
none of these
उत्तर
Figure is given as :
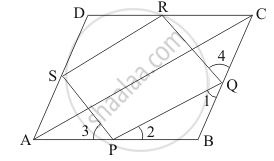
A rhombus ABCD is given in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively.
In ΔABC, P and Q are the mid-points AB and BC respectively.
Therefore,
PQ || AC and `PQ = 1/2 AC` ……(i)
Similarly, In ΔADC,R and S are the mid-points CD and AD respectively.
Therefore, SR || AC and `SR = 1/2 AC` ……(ii)
From (i) and (ii), we get
PQ|| SR and PQ = SR
Therefore, PQ RS is a parallelogram. …… (iii)
Now, we shall find one of the angles of a parallelogram.
Since ABCD is a rhombus
Therefore,
AB = BC (Sides of rhombus are equal)
`1/2 AB = 1/2 BC`
PB = BQ (P and Q are the mid-points AB and BC respectively)
In ΔPBQ, we have
PB = BQ
∠1 =∠2 (Angle opposite to equal sides are equal)
Therefore, ABCD is a rhombus
AB = BC
`1/2 AB = 1/2 BC`
AP = CQ …… (iii)
Also,
CD = AD
`1/2 CD = 1/2 AD`
CR = AS…… (iv)
Now, in ΔAPS and ,ΔCQR we have
AP = CQ [From (iii)]
CR = AS [From (iv)]
And PS = QR (PQRS is a parallelogram)
So by SSS criteria of congruence, we have
ΔAPS ≅ ΔCQR
By Corresponding parts of congruent triangles property we have:
∠3 = ∠4 …… (v)
Now, ∠1 +∠PQR + ∠4 = 180°
And ∠3 +∠SPQ +∠2 = 180°
Therefore,
∠3 +∠SPQ +∠2 = ∠1 +∠PQR +∠4 From (ii), we get ∠1 =∠2
From (v), we get ∠3 = ∠4
Therefore, ∠SPQ = ∠PQR…… (vi)
Now, transversal PQ cuts parallel lines SP and RQ at P and Q respectively.
∠SPQ +∠PQR = 180°
∠SPQ +∠SPQ = 180° [Using (vi)]
∠SPQ = 90°
Thus, PQRS is a parallelogram such that ∠SPQ = 90°.
Therefore, PQRS is a rectangle.
Hence the correct choice is (b).
APPEARS IN
संबंधित प्रश्न
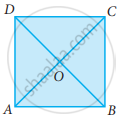
ABCD is a square. AC and BD intersect at O. State the measure of ∠AOB.
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
In a parallelogram ABCD, write the sum of angles A and B.
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following case, PQRS is a parallelogram?
∠P = 100°, ∠Q = 80°, ∠R = 95°
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°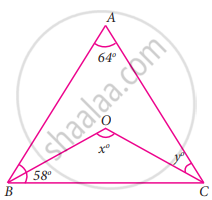
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are