Question

The figure formed by joining the mid-points of the adjacent sides of a rhombus is a

Options

•  square

• rectangle

• trapezium

• none of these

Answer 1

Figure is given as :

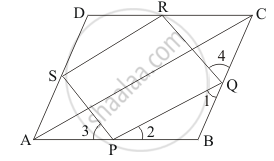
A rhombus ABCD is given in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively.

In ΔABC, P and Q are the mid-points AB and BC respectively.

Therefore,

 PQ || AC and `PQ = 1/2 AC` ……(i)

Similarly, In ΔADC,R and S are the mid-points CD and AD respectively.

Therefore, SR || AC and `SR = 1/2 AC` ……(ii)

From (i) and (ii), we get

PQ|| SR and PQ = SR

Therefore, PQ RS is a parallelogram. …… (iii)

Now, we shall find one of the angles of a parallelogram.

Since ABCD is a rhombus

Therefore,

 AB = BC (Sides of rhombus are equal)

`1/2 AB = 1/2 BC`

PB = BQ (P and Q are the mid-points AB and BC respectively)

In ΔPBQ, we have

PB = BQ

∠1 =∠2 (Angle opposite to equal sides are equal)

Therefore, ABCD is a rhombus

AB = BC

 `1/2 AB = 1/2 BC`

AP = CQ …… (iii)

Also,

CD = AD

`1/2 CD = 1/2 AD`

 CR = AS…… (iv)

Now, in ΔAPS and ,ΔCQR we have

 AP = CQ [From (iii)]

 CR = AS [From (iv)]

And PS = QR (PQRS is a parallelogram)

So by SSS criteria of congruence, we have

 ΔAPS ≅ ΔCQR

By Corresponding parts of congruent triangles property we have:

∠3 = ∠4 …… (v)

Now, ∠1 +∠PQR + ∠4 = 180°

And ∠3 +∠SPQ +∠2 = 180°

Therefore,

∠3 +∠SPQ +∠2 = ∠1 +∠PQR +∠4 From (ii), we get ∠1 =∠2

From (v), we get ∠3 = ∠4

Therefore, ∠SPQ = ∠PQR…… (vi)

Now, transversal PQ cuts parallel lines SP and RQ at P and Q respectively.

∠SPQ +∠PQR = 180°

 ∠SPQ +∠SPQ = 180° [Using (vi)]

∠SPQ = 90°

Thus, PQRS is a parallelogram such that ∠SPQ = 90°.

Therefore, PQRS is a rectangle.

Hence the correct choice is (b).