Advertisements
Advertisements
Question
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
Advertisements
Solution
Parallelogram ABCD is given as follows:
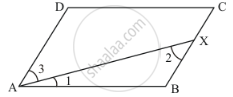
We have AX bisects ∠A bisecting BC at X.
That is, BX = CX
We need to find AB :AD
Since, AX is the bisector ∠A
That is,
`∠1 =1/2 ∠A ` …… (i)
Also, ABCD is a parallelogram
Therefore, AD || BC and AB intersects them
∠A +∠B = 180°
∠B = 180° - ∠A …… (ii)
In ΔABX,by angle sum property of a triangle:
∠1 +∠2 + ∠B = 180°
From (i) and (ii), we get:
`1/2 ∠A + ∠2 + 180° - ∠A = 180°`
`∠2- 1/2 ∠A = 0`
`∠2 = 1/2 ∠A` …… (iii)
From (i) and (iii),we get:
∠1 = ∠2
Sides opposite to equal angles are equal. Therefore,
BX = AB
2BX = 2AB
As X is the mid point of BC. Therefore,
BC = 2AB
Also, ABCD is a parallelogram, then, BC = AD
AD = 2AB
Thus,
AB :AD = AB :2AB
AB :AD = 1:2
Hence the ratio of AB : AD is 1:2.
APPEARS IN
RELATED QUESTIONS
In Fig., below, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
We get a rhombus by joining the mid-points of the sides of a
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are
